Una de las grandes contribuciones griegas al concepto mismo de la matemática fue el reconocimiento consciente y el énfasis puesto en el hecho de que los objetos matemáticos, números y figuras geométricas, son abstracciones, ideas producidas por la mente y claramente distintas de los objetos o imágenes físicas. Hemos visto, al estudiar la matemática de las civilizaciones primitivas, que los conceptos geométricos estaban ligados a la materia. Para los egipcios, por ejemplo, una recta no era más que una cuerda tensa o el borde de un terreno, y un rectángulo, su frontera.
El reconocimiento de que la matemática trabaja con abstracciones puede atribuirse con cierta seguridad a los pitagóricos; aunque puede que esto no sea cierto desde el principio. Según Aristóteles, los pitagóricos consideraban a los números como los componentes últimos de los objetos materiales del mundo real. Así pues, los números no tenían una existencia separada de los objetos sensibles. Cuando los primeros pitagóricos decían que todos los objetos estaban compuestos por números (entendidos estos como enteros), o que los números eran la esencia del universo, lo entendían en sentido literal, porque los números eran para ellos como los átomos para nosotros. Se supone incluso que los pitagóricos de los siglos VI y V no distinguían realmente los números de los puntos geométricos, entendidos, naturalmente, como puntos extensos o esferas minúsculas. Para Eudemo, Pitágoras fue el verdadero creador de la matemática pura, a la que convirtió en una arte liberal.
Los pitagóricos solían representar los números mediante puntos en la arena o piedrecillas, clasificándolos según las formas de estas distribuciones de puntos o piedras. Así, los números 1, 3, 6, 10, etc., recibían el nombre de triangulares porque los puntos correspondientes podían distribuirse en forma de triángulo equilátero. El cuarto número triangular, el 10, ejerció una fascinación especial sobre los pitagóricos, siendo para ellos una especie de número sagrado, que tiene cuatros puntos en cada lado; el 4 era otro de sus números favoritos. Los pitagóricos comprobaron que las sumas 1, 1+2, 1+2+3, y así sucesivamente, daban lugar a los números triangulares y que
Los números 1, 4, 9, 16, … recibieron el nombre de números cuadrados debido a que sus puntos pueden distribuirse formando cuadrados. Lo números no primos que no eran cuadrados perfectos recibían el nombre de oblongos.
A partir de las distribuciones geométricas de los puntos aparecían como evidentes ciertas propiedades de los números enteros; por ejemplo, trazando la recta que aparece en la figura de la izquierda se descubre que la suma de dos números triangulares consecutivos es un número cuadrado. Esto es verdad en general, como podemos ver en notación moderna:
Para pasar de un número cuadrado al siguiente, los pitagóricos seguían el esquema que aparace en la siguiente figura:
los puntos a la derecha y bajo las rectas en la figura forman lo que ellos llamaban un gnomon. Simbólicamente, lo que descubrieron era que:
Además, si partimos del 1 y añadimos el gnomon 3 y después el gnomon 5, y así sucesivamente, lo que tenemos es, en nuestro simbolismo:
Respecto a la palabra gnomon, probablemente significó al principio, en Babilonia, una varilla cuya sombra marcaba la hora. En la época de Pitágoras significaba una escuadra de carpintero, y esta es la forma del gnomon anterior.
Los pitagóricos estudiaron también los números poligonales, tales como los pentagonales, hexagonales y otros. El primer número pentagonal es el 1; el segundo, cuyos puntos forman los vértices de un pentágono, es el 5; el tercero es , y así sucesivamente. El n-ésimo número pentagonal es, en nuestra notación,
Análogamente, los números hexagonales son 1, 6, 15, 28, …, y en general:
Se llamó número perfecto a todo aquel que es igual a la suma de sus divisores, incluido el 1, pero no el propio número; por ejemplo, 6, 28, 496. A los que excedían a la suma de sus divisores se los llamó excesivos, y a los que eran menores que dicha suma, defectivos. A dos números se los llamó amigos, cuando cada uno de ellos era igual a la suma de los divisores del otro, por ejemplo, 284 y 220.
Los pitagóricos descubrieron una regla para construir ternas de números enteros que pudieran ser lados de un triángulo rectángulo. Así descubrieron que si es un número impar, entonces
 y
y  constituyen una de estas ternas. Sin embargo, esta regla solamente da algunas de ellas. Cualquier terna de números enteros que represente los lados de un triángulo rectángulo recibe el nombre de terna pitagórica.
constituyen una de estas ternas. Sin embargo, esta regla solamente da algunas de ellas. Cualquier terna de números enteros que represente los lados de un triángulo rectángulo recibe el nombre de terna pitagórica.Los pitagóricos estudiaron los números primos, las progresiones y ciertos tipos de razones y proporciones que encerraban para ellos una belleza especial. Para los pitagóricos, los números eran únicamente los números enteros y una razón entre dos números no era una fracción y, por lo tanto, otro tipo de número como en la época moderna. Las fracciones concretas, utilizadas para expresar partes de una unidad monetaria o de una medida, se utilizaban evidentemente en el comercio, pero tales usos comerciales de la aritmética quedaban fuera del marco de la matemática propiamente dicha. Por lo tanto, los pitagóricos se vieron desagradablemente sorprendidos por el descubrimiento de que algunas razones, por ejemplo, la razón de la hipotenusa de un triángulo rectángulo isósceles a un cateto o, lo que es lo mismo, de la diagonal al lado de un cuadrado, no podían expresarse por medio de números enteros.
Bibliografía
1. Boyer, Carl B.:"Historia de la matemática". Alianza Editorial, S.A., Madrid, 1999.
2. HEATH, T.L.: "A Manual of Greek Mathematics". Courier Dover Publications. 2003.
3. Klein, Carl B.:"El pensamiento matemático de la Antgüedad a nuestros días", vol I. Alianza Editorial, S.A., Madrid, 1992.
2. HEATH, T.L.: "A Manual of Greek Mathematics". Courier Dover Publications. 2003.
3. Klein, Carl B.:"El pensamiento matemático de la Antgüedad a nuestros días", vol I. Alianza Editorial, S.A., Madrid, 1992.
4. MacTutor History of Mathematics archive (página web en inglés).
Mª del Carmen Torres Alonso
Profesora Dpto. de Matemáticas








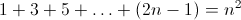




No hay comentarios:
Publicar un comentario